Tamilnadu State Board New Syllabus Samacheer Kalvi 11th Maths Guide Pdf Chapter 1 Sets, Relations and Functions Ex 1.3 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 1 Sets, Relations and Functions Ex 1.3
Question 1.
Suppose that 120 students are studying in 4 sections of eleventh standard in a school. Let A denote the set of students and B denote the set of the sections. Define a relation from A to B as “x related to y if the student x belongs to the section y”. Is this relation a function? What can you say about the inverse relation? Explain your answer.
Answer:
Given A denotes the set of students and B denotes the set of sections. Aslo given there 120 students and 4 sections.
Let f be a relation from A to B as “x related to y if the student x belongs to the section y”

Two are more students in A may belong to same section in B. But one student in A cannot belong to two or more sections in B. Every student in A can belong to any one of the section in B. Therefore / is a function.
In B we can have sections without students. Every element in B need not have preimage in A.
∴ f need not be onto.
Thus, f is a function and inverse relation for f need not exist.
![]()
Question 2.
Write the values of f at – 4, 1, -2, 7, 0 if

Answer:
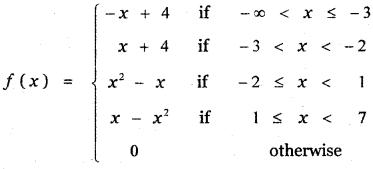
When x = -4
f(x) = – x + 4
f(-4) = – (-4) + 4
= 4 + 4 = 8
When x = 1
f(x) = x – x2
f(1) = 1 – 12
= 1 – 1 = 0
![]()
When x = -2
f(x) = x2 – x
f(-2) = (-2)2 – (-2)
= 4 + 2 = 6
When x – 7
f(x) = 0
⇒ f(7) = 0
When x = 0
f(x) = x2 – x
⇒ f(0) = 02 – 0 = 0
Question 3.
Write the values of f at – 3, 5, 2, – 1, 0 if
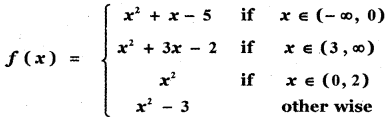
Answer:

When x = – 3
f(x) = x2 + x – 5
f(-3) = (-3)2 + (-3) – 5
= 9 – 3 – 5
= 9 – 8 = 1
When x = 5
f(x) = x2 + 3x – 2
f(5) = 52 + 3(5) – 2
= 25 + 15 – 2
= 40 – 2 = 38
![]()
When x = 2
f(x) = x2 – 3
f(2) = 22 – 3 = 4 – 3 = 1
When x = – 1
f(x) = x2 + x – 5
f(-1) = (-1)2 – 1 – 5 = 1 – 1 – 5 = – 5
When x = 0
f(x) = x2 – 3
f(0) = 02 – 3
Question 4.
State whether the following relations are functions or not. If it is a function, check for one – to – oneness and ontoness. If it is not a function, state why?
(i) If A = { a, b, c } and f = { (a, c), (b, c), (c, b) }; (f : A → A)
Answer:
A = { a, b, c }
f = {(a, c), (b, c), (c, b)}; f : A → A

f is a function since every element in the domain has a unique image in the codomain.
f is not one-one.
a, b belonging to the domain A has the same image in the codomain A. f is not onto since belonging to the codomain A does not have preimage in the domain A Thus the relation / is a function from A to A and it is neither one-one nor onto.
(ii) If X = { x, y, z } and f = { (x, y), (x, z), (z, x) }; (f: X → X)
Answer:
X = { x, y, z }
f = {(x, y), (x, z), (z , x) } f : X → X

The relation f: X → X is not a function since the element x in the domain has two images in the co-domain.
![]()
Question 5.
Let A = {1, 2, 3, 4} and B = { a, b , c, d } Give a function from A → B for each of the following.
(i) neither one-to-one nor onto.
Answer:

f = { (1, b) , (2, c) , (3, d) , (4, d)
f is a function, it not one to one and not onto.
(ii) not one – to – one but onto
Answer:
Does not exists
(iii) one – to – one but not onto
Answer:
Does not exist
(iv) one – to – one and onto
Answer:

f = { (1, a) , (2, b) , (3, c) , (4, d) }
f is a function which is one – to – one and onto.
![]()
Question 6.
Find the domain of \(\frac{1}{1-2 \sin x}\)
Answer:
Let f(x) = \(\frac{1}{1-2 \sin x}\)
When 1 – 2 sin x = 0
⇒ 1 = 2 sin x
sin x = \(\frac{1}{2}\)
⇒ sin x = sin \(\left(\frac{\pi}{6}\right)\)
x = nπ + (- 1)n\(\frac{\pi}{6}\), n ∈ Z
sin x = sin α ⇒ x = nπ + (-1)nd, n ∈ Z
∴ Domain of f(x) is

Question 7.
Find the largest possible domain of the real valued function f(x) = \(\frac{\sqrt{4-x^{2}}}{\sqrt{x^{2}-9}}\)
Answer:

∴ For no real values of x, f (x) is defined.
∴ Domain of f(x) = { }
![]()
Question 8.
Find the range of the function \(\frac{1}{2 \cos x-1}\)
Answer:
Let f(x) = \(\frac{1}{2 \cos x-1}\)
Range of cosine function is
– 1 ≤ cos x ≤ 1
– 2 ≤ 2 cos x ≤ 2
– 1 ≤ 2 cos x – 1 ≤ 2 – 1
– 3 ≤ 2 cos x – 1 ≤ 1
\(-\frac{1}{3}\) ≥ \(\frac{1}{2 \cos x-1}\) ≥ 1

Question 9.
Show that the relation xy = – 2 is a function for a suitable domain. Find the domain and the range of the function.
Answer:
xy = – 2 ⇒ y = -2/x
which is a function
The domain is (-∞, 0) ∪ (0, ∞) and range is R – {0}
![]()
Question 10.
If f, g : R → R are defined by f(x) = |x| + x and g(x) = |x| – x find gof and fog.
Answer:
Given

![]()
Question 11.
If f, g, h are real-valued functions defined on R, then prove that (f + g)oh = foh + goh what can you say about fo(g + h )? Justify your answer.
Answer:
Given f : R → R , g : R → R and h : R → R (f + g) oh: R → R and (f o h + g o h) : R → R for any x ∈ R.
[(f + g)oh] (x) = (f + g) h(x)
= f(h(x)) + g(h(x))
= foh(x) + goh(x)
∴ (f + g)oh = foh + goh
Also fo(g + h)(x) = f((g + h)(x)) for any x ∈ R
= f(g(x) + h(x))
= f(g(x)) + f(h(x))
= fog (x) + foh(x)
∴ fo(g + h) = fog +foh
Question 12.
If f : R → R is defined by f( x ) = 3x – 5, Prove that f is a bijection and find its inverse.
Answer:
Given f(x) = 3x – 5
Let y = 3x – 5
y + 5 = 3x
⇒ \(\frac{y+5}{3}\) = x
Let g(y) = \(\frac{y+5}{3}\)
gof (x) = g(f(x))
= g(3x – 5)
= \(\frac{3 x-5+5}{3}\) = \(\frac{3 x}{3}\) = x
gof (x) = x
fog (y) = f(g(y))
= f\(\left(\frac{y+5}{3}\right)\)
= 3\(\left(\frac{y+5}{3}\right)\) – 5
= y + 5 – 5
fog(y) = y
∴ gof = Ix and fog = IY
Hence f and g are bijections and inverses to each ot1er.
Hence f is a bijection and f-1(y) = \(\frac{y+5}{3}\)
Replacing y by x we get f-1(x) = \(\frac{x+5}{3}\)
![]()
Question 13.
The weight of the muscles of a man is a function of his bodyweight x and can be expressed as W ( x ) = 0.35x. Determine the domain of this function.
Answer:
W(x) = 0.35x
Since bodyweight x is positive and if it increases then W(x) also increases.
Domain is (0, ∞) i.e.,x > 0
Question 14.
The distance of an object falling is a function of time t and can be expressed as s ( t) = – 16t2. Graph the function and determine if it is one – to – one.
Answer:
Given s (t) = – 16t2
s (t1) = s (t2) ⇒ – 16t12 = – 16t22
⇒ t12 = t22
⇒ ± t1 = ± t2
Since s (t1) = s (t1) ![]() 14 t1 = t2
14 t1 = t2
∴ The function s(t) is not one-one
Graph of s(t) = – 16t2
Take the time along x – axis and distance along y – axis.

![]()
Question 15.
The total cost of airfare on a given route is comprised of the base cost C and the fuel Surcharge S in rupee. Both C and S are functions of the mileage m; C ( m ) = 0.4 m + 50 and S ( m ) = 0.03m. Determine a function for the total cost of a ticket in terms of the mileage and find the airfare for flying 1600 miles.
Answer:
C – base cost,
S = fuel surcharge,
m = mileage
C(m) = 0.4 m + 50
S(m) = 0.03 m
Total cost = C(m) + S(m)
= 0.4 m + 50 + 0.03 m
= 0.43 m + 50
for 1600 miles
T(c) = 0.43 (1600) + 50 = 688 + 50 = ₹ 738
Question 16.
A salesperson whose annual earnings can be represented by the function A (x) = 30,000 + 0.04 x, where x is the rupee value of the merchandise, he sells. His son is also in sales and his earnings are represented by the function S(x) = 25,000 + 0.05 x. Find (A + S)(x) and determine the total family income if they each sell Rs. 1,50,00,000 worth of merchandise.
Answer:
Given A (x) = 30,000 + 0.04 x
S (x) = 25,000 + 0.05x
A(x) + S(x) = 30,000 + 0.04 x + 25,000 + 0.05x
(A + S)(x) = 55,000 + 0.09 x
Given x = 1,50,00,000
Then (A + S)(x) = 55000 + 0.09 × 1,50,00,000
= 55000 + 1,35000000
Total family income = Rs. 14,05,000
![]()
Question 17.
The function for exchanging American dollars for Singapore Dollar on a given day is f (x) = 1.23x, where x represents the number of American dollars. On the same day, the function for exchanging Singapore Dollar to Indian Rupee is g(y) = 50.50y, where y represents the number of Singapore dollars. Write a function which will give the exchange rate of American dollars in terms of Indian rupee.
Answer:
Given f(x) = 1.23x
where x represents the number of American dollars
g(y) = 50.50y
where y represents the number of Singapore dollars.

To convert American dollars to Indian rupees, we must find
gof (x) = g(f(x))
= g (1.23x)
= 50.50 (1.23x)
= 62.115x
∴ The function for the exchange rate of American can dollars in terms of Indian rupees is
gof (x) = 62.1 15x
Question 18.
The owner of a small restaurant can prepare a particular meal at a cost of Rs. 100. He estimates that if the menu price of the meal is x rupees, then the number of customers who will order that meal at that price in an evening is given by the function D (x) = 200 – x. Express his day revenue total cost and profit on this meal as functions of x.
Answer:
cost of one meal = ₹ 100
Total cost = ₹ 100 (200 – x)
Number of customers = 200 – x
Day revenue = ₹ (200 – x) x
Total profit = day revenue – total cost
= (200 – x) x – (100) (200 – x)
![]()
Question 19.
The formula for converting from Fahrenheit to Celsius temperature is y = \(\). Find the inverse of this function and determine whether the inverse is also a function?
Answer:


![]()
Question 20.
A simple cipher takes a number and codes it, using the function f( x) = 3x – 4. Find the inverse of this function, determine whether the inverse is also a function and verify the symmetrical property about the line y = x (by drawing the lines)
Answer:
Given f(x) = 3x – 4
Let y = 3x – 4
⇒ y + 4 = 3x
⇒ x = \(\frac{y+4}{3}\)
Let g(y) = \(\frac{y+4}{3}\)
gof (x) = g (f(x) )
= g(3x – 4)
= \(\frac{3 x-4+4}{3}=\frac{3 x}{3}\)
gof(x) = x
and fog(y) = f(g(y))
= f\(\left(\frac{y+4}{3}\right)\)
= 3\(\left(\frac{y+4}{3}\right)\)
= y + 4 – 4 = y
fog (y) = y
Hence g of = Ix and fog = Iy
This shows that f and g are bijections and inverses of each other.
Hence f is bijection and f-1(y) = \(\frac{y+4}{3}\)
Replacing y by x we get f-1(x) = \(\frac{x+4}{3}\)
The line y = x

f(x) =
The line y =3x-4
When x = 0 ⇒ y = 3 × 0 – 4 = -4
When x = 1 ⇒ y = 3 × 1 – 4 = -1
When x = -1 ⇒ y = 3 × -1 – 4 = -7
When x = 2 ⇒ y = 3 × 2 – 4 = 2
When x = -2 ⇒ y = 3 × -2 – 4 = -10
When x = 3 ⇒ y = 3 × 3 – 4 = 5
When x = -3 ⇒ y = 3 × -3 – 4 = -13

![]()
The line y = \(\frac{x+4}{3}\)

