Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 3 Algebra Ex 3.6 Text Book Back Questions and Answers, Notes.
Tamilnadu Samacheer Kalvi 8th Maths Solutions Chapter 3 Algebra Ex 3.6
To find the value of x, bring the variable to the left side and bring all the remaining values to the right side. Simplify the values to find the result.
Question 1.
Fill in the blanks:
(i) The value of x in the equation x + 5 = 12 is ________ .
Answer:
7
Hint:
Given, x + 5 = 12
x = 12 – 5 = 7 (by transposition method)
Value of x is 7
![]()
(ii) The value of y in the equation y – 9 = (-5) + 7 is ________ .
Answer:
11
Hint:
Given, y – 9 = (-5) + 7
y – 9 = 7 – 5 (re-arranging)
y – 9 = 2
∴ y = 2 + 9 = 11 (by transposition method)
(iii) The value of m in the equation 8m = 56 is ________ .
Answer:
7
Hint:
Given, 8m = 56
Divided by 8 on both sides
\(\frac{8 \times m}{8}=\frac{56}{8}\)
∴ m = 7
![]()
(iv) The value of p in the equation \(\frac{2 p}{3}\) = 10 is ________ .
Answer:
15
Hint:
Given, \(\frac{2 p}{3}\) = 10
Multiplying by 3 on both sides

Dividing by 2 on both sides

∴ p = 15
(v) The linear equation in one variable has ________ solution.
Answer:
one
Question 2.
Say True or False.
(i) The shifting of a number from one side of an equation to other is called transposition.
Answer:
True
(ii) Linear equation in one variable has only one variable with power 2.
Answer:
False
[Linear equation in one variable has only one variable with power one – correct statement]
![]()
Question 3.
Match the following

(A) (i),(ii), (iv) ,(iii),(v)
(B) (iii), (iv), (i) ,(ii), (v)
(C) (iii),(i) ,(iv), (v), (ii)
(D) (iii) , (i) , (v) ,(iv) ,(ii)
Answer:
(C) (iii),(i) ,(iv), (v), (ii)
a. \(\frac{x}{2}\) = 10, multiplying by 2 on both sides, we get
\(\frac{x}{2}\) × 2 = 10 × 2 ⇒ x = 20
b. 20 = 6x – 4 by transposition ⇒ 20 + 4 =6x
6x = 24 dividing by 6 on both sides,
\(\frac{6 x}{6}=\frac{24}{6}\) ⇒ x = 4
c. 2x – 5 = 3 – x
By transposing the variable ‘x’, we get
2x – 5 + x = 3
by transposing – 5 to other side,
2x + x = 3 + 5

∴ x = \(\frac{8}{3}\)
d. 7x – 4 – 8x = 20
by transposing – 4 to other side,
7x – 8x = 20 + 4
– x = 24
∴ x = – 24
e. \(\frac{4}{11}-x=\frac{-7}{11}\)
Transposing \(\frac{4}{11}\) to other side,
– x = \(\frac{-7}{11} \frac{-4}{11}=\frac{-7-4}{11}=\frac{-11}{11}\) = – 1
∴ – x = – 1 ⇒ x = 1
![]()
Question 4.
Find x:
(i) \(\frac{2 x}{3}-4=\frac{10}{3}\)
Answer:
Transposing – 4 to other side, it becomes + 4

(ii) \(y+\frac{1}{6}-3 y=\frac{2}{3}\)
Answer:
Transposing \(\) to the other side,

![]()
(iii) \(\frac{1}{3}-\frac{x}{3}=\frac{7 x}{12}+\frac{5}{4}\)
Answer:
Transposing \(\frac{-x}{3}\) to the other side, it becomes + \(\frac{x}{3}\)
∴ \(\frac{1}{3}=\frac{7 x}{12}+\frac{5}{4}+\frac{x}{3}\)
Transposing \(\frac{5}{4}\) to the other side, it becomes \(\frac{-5}{4}\)
\(\frac{1}{3}-\frac{5}{4}=\frac{7 x}{12}+\frac{x}{3}\)
Multiply by 12 throughout [we look at the denominators 3, 4, 12, 3 and take the LCM, which is 12]

4 – 15 = 7x + x × 4
– 11 = 7x + 4x
11x = – 11
x = -1
Question 5.
Find x
(i) -3(4x + 9) = 21
Answer:
![]()
Expanding the bracket,
-3 × 4 + (-3) × 9 = 21
∴ -12x + (-27) = 21
– 12x – 27 = 21
Transposing – 27 to other side, it becomes +27
– 12 x = 21 + 27 = 48
∴ – 12x = 48 ⇒ 12x = – 48
Dividing by 12 on both sides

![]()
(ii) 20 – 2 (5 – p) = 8
Answer:
![]()
Expanding the bracket,
20 – 2 × 5 – 2 × (-p) = 8
20 – 10 + 2p = 8
(- 2 × – p = 2p)
10 + 2p = 8 transposing lo to other side
2p = 8 – 10 = – 2
∴ 2p = – 2
∴ p = – 1
(iii) (7x – 5) – 4(2 + 5x) = 10(2 – x)
Answer:
![]()
Expanding the brackets,
7x – 5 – 4 × 2 – 4 × 5x = 10 × 2 + 10 × (-x)
7x – 5 – 8 – 20x = 20 – 10x
7x – 13 – 20x = 20 – 10x
Transposing 10x & – 13, we get
7x – 13 – 20x + 10x = 20
7x – 20x + 10x = 20 + 13, Simplifying,
– 3x = 33
3x = – 33
x = \(\frac{-33}{3}\) = – 11
x = – 11
![]()
Question 6.
Find x and m:
(i) \(\frac{3 x-2}{4}-\frac{(x-3)}{5}=-1\)
Answer:
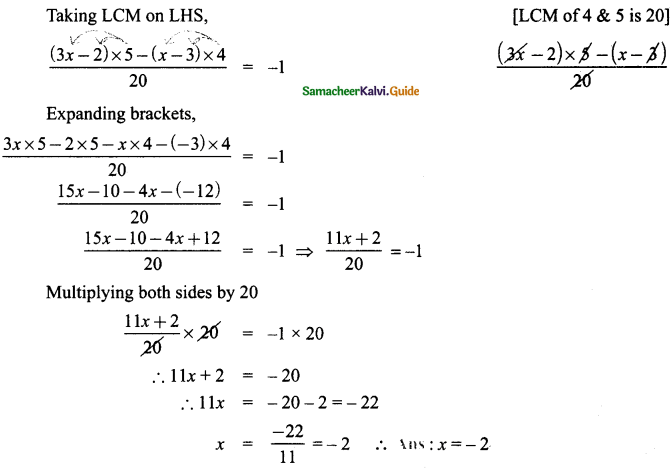
![]()
(ii) \(\frac{m+9}{3 m+15}=\frac{5}{3}\)
Answer:
Cross multiplying, we get


∴ (m + 9) × 3 = 5 × (3m + 15)
m × 3 + 9 × 3 = 5 × 3m + 5 × 15

27 – 75 = 15m – 3m
– 48 = 12m

⇒ m = – 4